Download From MediaFire: -------------------------------------------------------------------- http://www.mediafire.com/download.php?jfsshuzjwatvhoh --------------------------------------------------------------------
Download From This Site: -------------------------------------------------------------------------- http://m484games.ucoz.com/Games/Gods_Calculator_v131.zip --------------------------------------------------------------------------
System Requirements: Windows PC Programmed with: Liberty Basic Author: Master484 ____________________
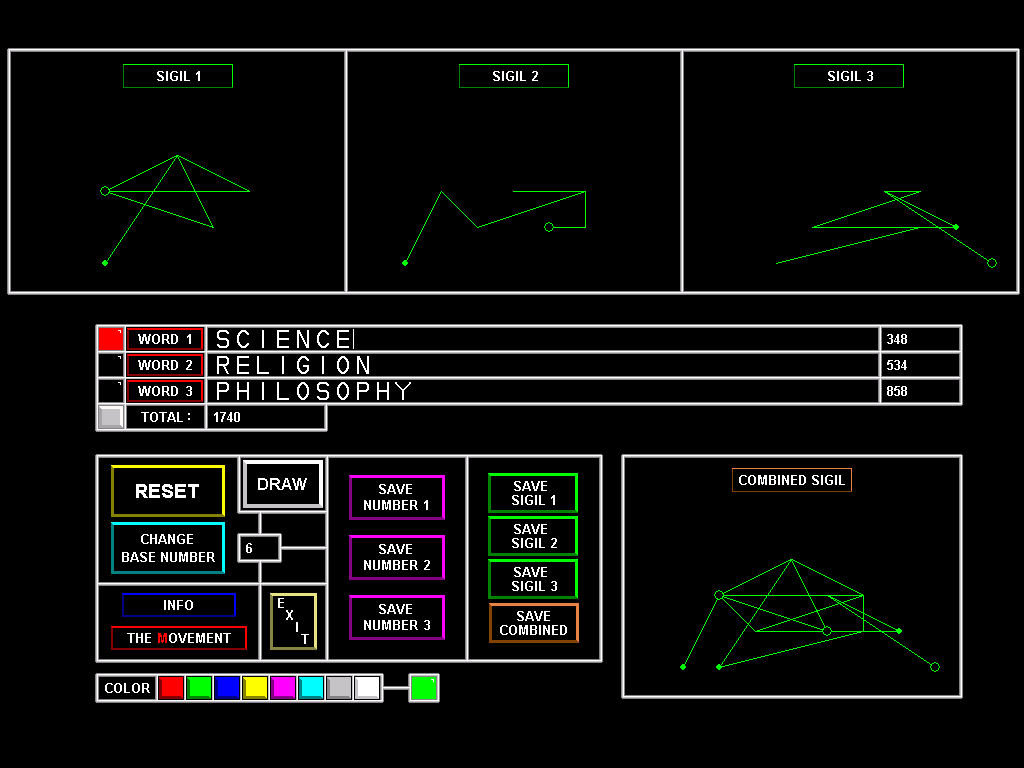
God's Calculator is a numerology/sigil drawing system. Enter any words into the program, and it transforms them into numeric values and magical sigils. Here is your chance to "hack reality" and to see "the codes of the matrix" with your own eyes. But great intuition and patience is required in order to understand those codes.
The program consists of two occult systems: God's Calculator and God's Pyramid.
The first one of these systems, the "God's Calculator", has been "revealed" to the public ages ago. It's the classic english gematria system which is based on number six. In it every letter of the alphabet is given a number equivalent in the following fashion:
A = 6 B = 12 C = 18 D = 24 E = 30 F = 36 G = 42 H = 48 I = 54 J = 60 K = 66 L = 72 M = 78 N = 84 O = 90 P = 96 Q = 102 R = 108 S = 114 T = 120 U = 126 V = 132 W = 138 X = 144 Y = 150 Z = 156
To find out some word's numeric value, you simply add all letter values together. For example, to find out the value of the word "computer", you just make the following calculation:
C = 18 : O = 90 : M = 78 : P = 96 : U = 126 : T = 120 : E = 30 : R = 108
18 + 90 + 78 + 96 + 126 + 120 + 30 + 108 = 666
Computer = 666
---
The second system in the program, the "God's Pyramid", has never been publicly released before the launch of this program, which was in December 2010. The God's Pyramid is a sigil making method, where all letters of the alphabet are arranged to form a pyramid in the following fashion:
The sigil is started by drawing a dot at the first letter, and after that all letters in the word are joined one by one with a line. Then the sigil is finished by drawing a circle at the last letter.
A more accurate explanation on how these system work can be found in the program's manual. Although knowing that isn't necessary, unless you are intending to do the number counting and sigil drawing by hand. Because the program of course does all drawing and counting for you, when you give the words to it.
And finally, here's a video which shows how it works:
